2月5日，《计算物理杂志》（Journal of Computational Physics）在线发表了sunbet中国官网柴振华教授团队的最新研究成果“Regularized lattice Boltzmann method based maximum principle and energy stability preserving finite-difference scheme for the Allen-Cahn equation”。柴振华教授为通讯作者，我们2024级博士研究生陈颖为第一作者，其他参与者包括刘茜博士和施保昌教授。

 Allen-Cahn方程作为一类经典的相场模型，在晶体生长、界面动力学、图像处理等领域具有广泛应用。该方程具有两个关键性质：最大值原理（解的有界性）和能量耗散律。如何在离散数值方法中保持这两个性质，是设计保结构算法的主要挑战。近年来，介观格子Boltzmann（LB）方法被广泛用于求解相场模型，包括Allen-Cahn和Cahn-Hilliard方程，然而无法从理论上证明其具有保结构性质。本研究针对Allen-Cahn方程，首次提出了一种基于正则化LB方法的高效保结构有限差分格式，较传统LB方法，其具有两个方面的优势：（1）当时间步长满足一定条件时，该格式具有最大值原理和能量耗散性质（见图1）；（2）降低了存储空间，提高了计算效率（见表1）。

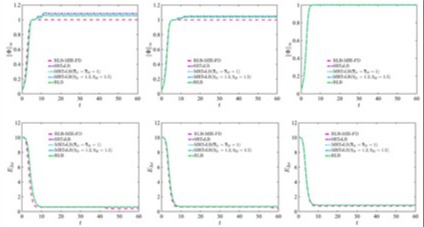
图1. 不同方法数值解的最大模和能量演化对比

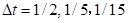
(从左至右)

表1. 内存使用量和CPU时间(s)对比

 该工作通过融合介观LB方法与宏观有限差分格式，为相场方程的高效计算提供了新思路。未来，团队计划将该研究拓展至Cahn-Hilliard方程与Navier-Stokes方程，推动其在复杂流体问题研究中的应用。

 论文链接：https://www.sciencedirect.com/science/article/pii/S0021999125001147