3月5日，SIAM Journal on Scientific Computing在线发表了柴振华教授团队的最新研究成果“A consistent and conservative diffuse-domain lattice Boltzmann method for multiphase flows in complex geometries”。柴振华教授为通讯作者，刘茜博士为第一作者，其他参与者包括我们博士研究生湛承杰、陈颖和施保昌教授。

       多相流问题广泛存在于能源、环境、材料、机械、航空航天等领域，基于相场模型的数值方法为研究这类复杂问题提供了有效工具。然而，针对多孔介质等非规则区域内的多相流动，如何有效处理流固边界条件成为当前数值模拟面临的一大挑战。为克服直接离散复杂边界条件带来的困难，扩散域（Diffuse Domain, DD）方法假设流体和固体的区域边界是具有一定厚度的扩散界面，在包括固体的更大区域上对原始数学模型进行重构，并借助渐近分析方法确定模型中体现流固边界条件影响的惩罚项。团队前期结合格子Boltzmann（Lattice Boltzmann, LB）方法的并行优势，构建了复杂区域两相流动的DD-LB模型[Liu et al., Multiscale Model. Simul., 20: 1411-1436 (2022)]。在此基础上，该工作进一步发展了多相润湿问题的DD-LB模型，并利用其研究了复杂区域内具有不同润湿特性的多相流动行为（见图1）。此外，该工作还推导了四相复合液滴平衡状态的解析解，为验证数值方法提供了基准问题。

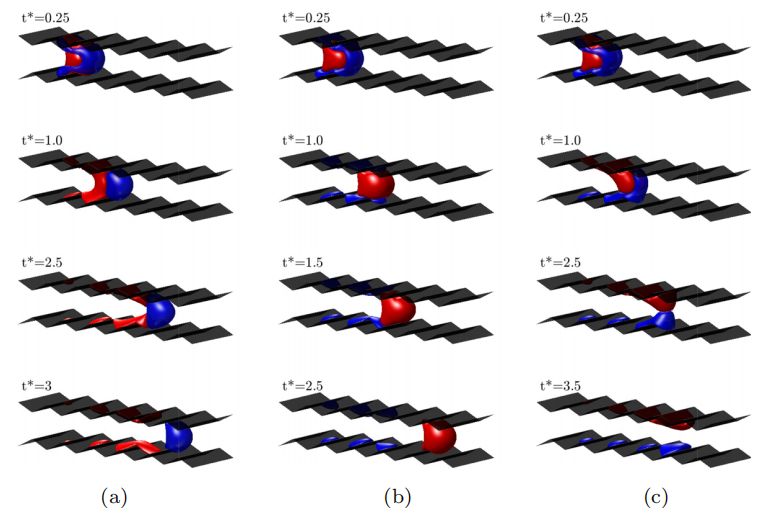
图1. 复杂管道中三相复合液滴输运过程

 该工作通过耦合扩散域和LB方法，为研究复杂区域内多相流问题提供了新的有效手段。未来，团队计划将该研究拓展至多孔介质内的多相流动问题。

 论文链接：https://epubs.siam.org/doi/10.1137/23M1599562